不用伽利略变换也能得到c+v和c-v
有人告诉我说:“利用距离时间和速度之间的关系,无需利用伽利略变换,我们就可以推导出c+v和c-v。所以你所说的相对论的自我矛盾并不存在。”
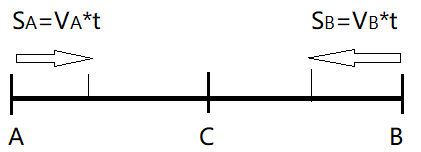
这个推导非常简单。如图所示,A和B分别以速度VA和VB沿同一直线在向C靠近,我们可以这样得到A和B之间的相对速度:
经过时间间隔t,A走过的距离是SA=VA*t,B走过的距离是SB=VB*t。根据速度的定义,A和B之间的相对速度就是
V = (SA+SB)/t = (VA*t+VB*t)/t = VA+VB
上述推导是否说明我们根本不需要伽利略速度变换呢?
不。以上的推导正是伽利略速度变换的来源。如果非要对这个推导过程说点什么,我们可以这样说:这个推导过程说明了牛顿的时空观是多么的自然。
当然,你可能使用略微不同的场景来说明伽利略速度变换。在《相对论:狭义和广义理论》第一部分的第六节:“经典力学中的速度相加公式”中,爱因斯坦就使用了行走在列车上的人作为例子。对于所有的例子,我们都能用同样的方法轻松地得出速度叠加公式,这就是伽利略速度变换公式。
所以,伽利略速度变换只是一个简便法。有了它,我们就可以随时使用,而不用每次都再重新推导一遍。你还记得小学数学里的相遇问题和追及问题吗?我们当时用的就是这个简便法,只不过我们并不知道它的名字。
如何得出这个公式并不重要,把它叫做什么也不重要,重要的是它背后所依赖的概念。脱离了牛顿的时空观,也就是均匀的空间和时间,以上公式就没有任何意义。
到目前为止,我们只有两个速度叠加规则:一个是伽利略规则,另一个是相对论规则。
在相对论诞生之前,只有伽利略规则,所以相对论的第一公式中的c+v和c-v只能来自伽利略规则。
在牛顿系统中,只有伽利略规则适用。在相对论中,只有相对论规则适用。相对论的推导过程使用了伽利略规则,所以它必定是错的。