c+v and c-v can be obtained without using Galilean transformation

Someone told me: "We can derive c+v and c-v using the distance, time and velocity relation, without using the Galilean transformation, so your claimed contradiction in Special Relativity does not exist."

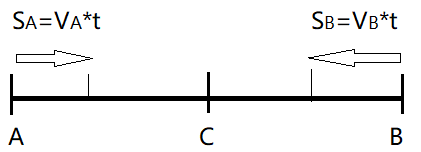
The derivation is easy. Like shown above, A and B are moving toward C at speed of V_A and V_B respectively, we can get the relative speed between A and B this way:

In a time interval of t, A covers a distance of S_A=V_A*t, and B covers a distance of S_B=V_B*t, so the relative speed between A and B is V = (S_A+S_B)/t = (V_A*t+V_B*t)/t = V_A+V_B

Does the above derivation of velocity addition formula mean we don't need Galilean transformation?

No. The above derivation is exactly how Galilean transformation is obtained. If we must say anything about it, we have to say it shows us how natural the Newtonian space and time concept is.

Of course, you may have used a slightly different senario to derive the formula. In section 06. "THE THEOREM OF THE ADDITION OF VELOCITIES EMPLOYED IN CLASSICAL MECHANICS", part I of "Relativity: The Special and General Theory", Einstein used a man walking in a moving train as an example. In all situations, we can derive the same formula with the same easiness.

So, Galilean transformation is only a shortcut. When handling relative motions along a straight line, we can always use this shortcut, saving ourselves the trouble of deriving the formula again and again. This formula can even be used in non-straight line cases, like we did for chase problems in elementary school.

It does not matter how we get the formula, and it does not matter how we call it. The only important thing is the concept behind it. Without the Newtonian space and time concept, which claims evenly distributed space and time, the above derivation and formula make no sense.

Until now, there are only two velocity addition rules: the Galilean rule and the Special Relativity rule. Before the birth of Special Relativity, the Galilean rule is the only one available. So the c+v and c-v in the first equation of Special Relativity must be Galilean transformation.

In a newtonian system, only the Galilean rule works. Under Special Relativity, only the Special Relativity rule works. Special Relativity mixed these two rules up, so it must be wrong.