The relative speed between the two spaceships can be 2c and c at the same time

This is what he means: Seen from the Earth, the two spaceships have a relative speed of 2c. And to an observer on any of the spaceships, their relative speed is c.

Here we will provide a mathematical prove: nomatter where the observer is, the relative speed between the two spaceships is always c. Here the settings are the same as in the paper, except that the speeds are v and w instead of c.

Case 1: Suppose we are on spaceship A. So the Earth is approaching us with speed v, and spaceship B is approaching the Earth with speed w. Here we can use the transformation formula directly:

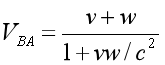
Case 2: Suppose we are on Earth. So spaceship A is approaching us with speed v from the left, and spaceship B is approaching us with speed w from the right. 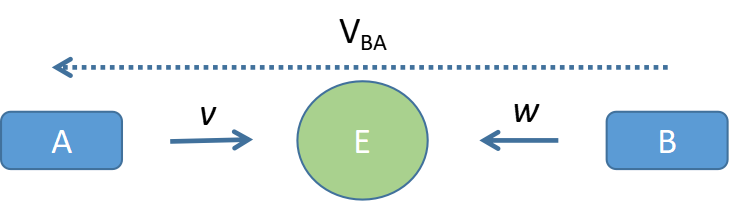This is the so called inapplicable case for Special Relativity.
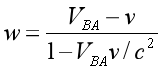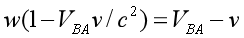
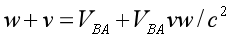
If we treat spaceship A as an intermediate reference frame, and suppose spaceship B is approaching spaceship A with an unknown speed V_BA from the right, then we can apply the transformation of Special Relativity, like shown below: Here we added negative sign in front of v, as the direction of v is opposite to the direction of the other two speeds. With some simple transformation, 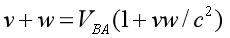we can get the relative speed V_BA between spaceship A and B: 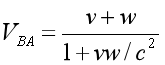Thus we can see, this speed is exactly the same as what we have obtained when we are in spaceship A.

So, under Special Relativity, there is only one velocity addition rule. Just like in Newtonian system, the only veloctiy addition rule is Galileo transformation.