Time dilation formula can be obtained without using c+v and c-v

When talking about Special Relativity to the general public, many people use a triangle to derive the time dilation formula.

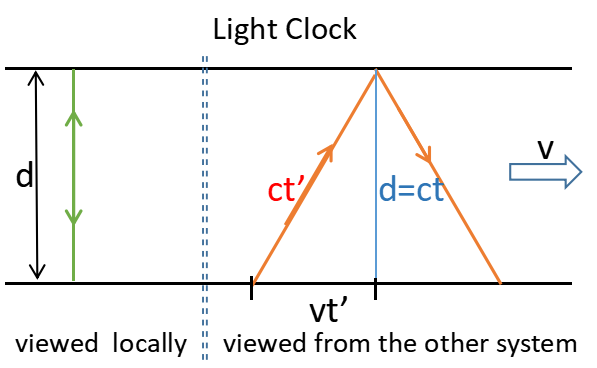
Like shown in the diagram, there are two reference frames, one is "stationary", and the other is moving at the speed of v. In the moving system, there is a light clock, whose light rays are perpendicular to the direction of v. The distance between the two reflecting surfaces is d.

When observed in the moving system(where the clock is located), it takes time t for the light ray to leave one surface and reach the other surface.

But when observed in the "stationary" system, the situation is different. While the light ray is trying to reach the other surface of the clock, the other surface is also moving away at the speed of v, so the light ray has to travel a longer distance.

Using a little knowlege of geometry, we can get (ct')²=(vt')²+(ct)². With a simple manipulation, we get the time dilation formula:

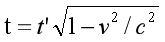
Since c+v and c-v are not used here, the contradiction of Special Relativity is avoided, right?

Probably not.

If you have time to browse through Einstein's paper on Special Relativity, you will see no triangle is involved. So although we get the same formula here, this derivation may have nothing to do at all with Special Relativity.

Have you ever tried to read a clock in an airplane flying over your head? It seems so strange to me, I guess no one has ever done it before.

Based on Special Relativity, length contraction happens in the direction of motion. In the triangle shown above, the length along the v direction is contracted, but the length perpendicular to v direction is not. So we have no way to use the Pythagorean theorem.

For the same reason, the derivation of c+v and c-v makes no sense under Special Relativity. Because we don't know how to add two distances, if one is contracted by a factor of α and the other is contracted by a factor of β.