相对论的第一假定 (3)

假设在某一惯性参照系中，有一个关于牛顿第二运动定律的实验正在进行。

我们要证明的是：在任意选取的两个惯性参照系A和B中，F=ma都成立。

因为参照系A和B都是虚拟的，它们对于实验的m和F都没有影响，所以我们要证明的就是，从两个参照系所得的加速度是相等的。

在参照系Ａ中，得到的加速度是：

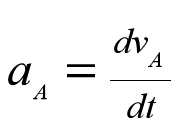
在参照系Ｂ中，得到的加速度是：

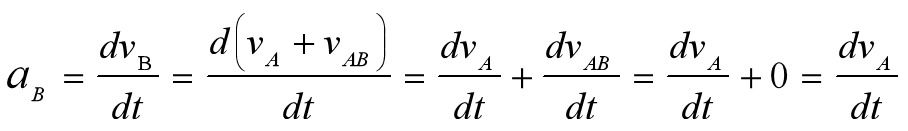
其中 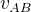是参照系Ａ相对于参照系Ｂ的速度。因为两个参照系都是惯性参照系，所以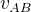是一个常数，它对时间的变化率为零。

以上的推导证明了，两个参照系中得出的加速度确实相同。
换句话说，牛顿第二定律在两个参照系中的表达形式确实是完全一样的。

在前面的证明中，我们利用了伽利略速度变换：

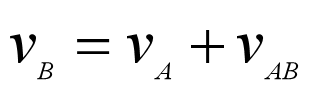
这就是我们在高中物理课上所学的速度变换公式，该公式代表的就是相对运动。 所以一个隐藏在第一假定后面的条件就是：

所有的运动都是相对运动。