On Velocity Addition (2)

Let's work on a simple math problem.
Two children are walking toward each other, when will they meet?

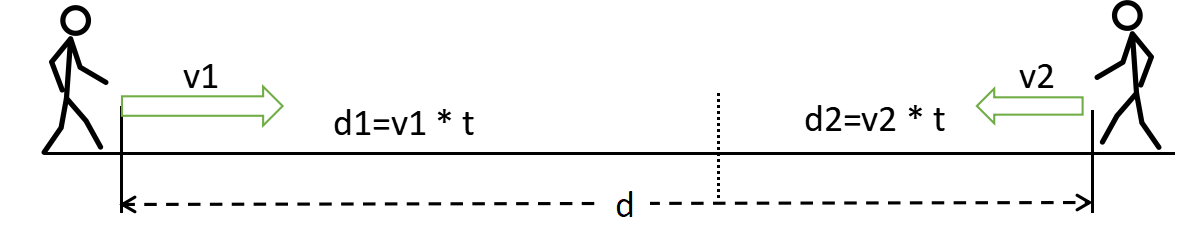
Assume they will meet after time t. During this time, the first child will have walked a distance of d1=v1*t, and the second child will have walked a distance of d2=v2*t. Since d1+d2=d, so we have v1*t + v2*t =d, thus (v1+v2) * t= d, and finally we get t=d/(v1+v2).

In this example, we used the following definitions and assumptions (maybe unknowingly):

Definitions:
     Distance, Time, and Speed (Speed=Distance/Time)

Assumptions:

1. Evenly distributed space (so we can have d=d1+d2)
2. Evenly flowing time (so in the example, we don’t care it is today or tomorrow, at noon or in the evening)
3. Any distance or time interval has the same measurement in all reference frames. (so the two children’s time are the same, and their distances walked can be added up).